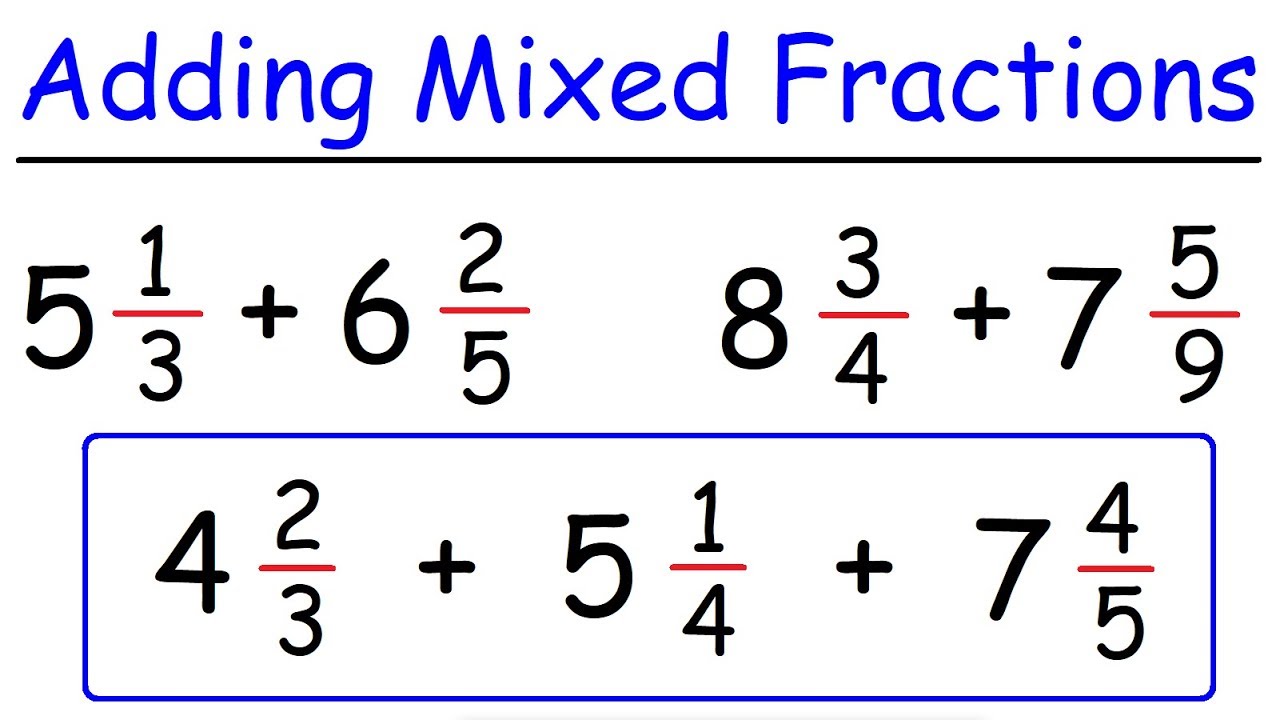
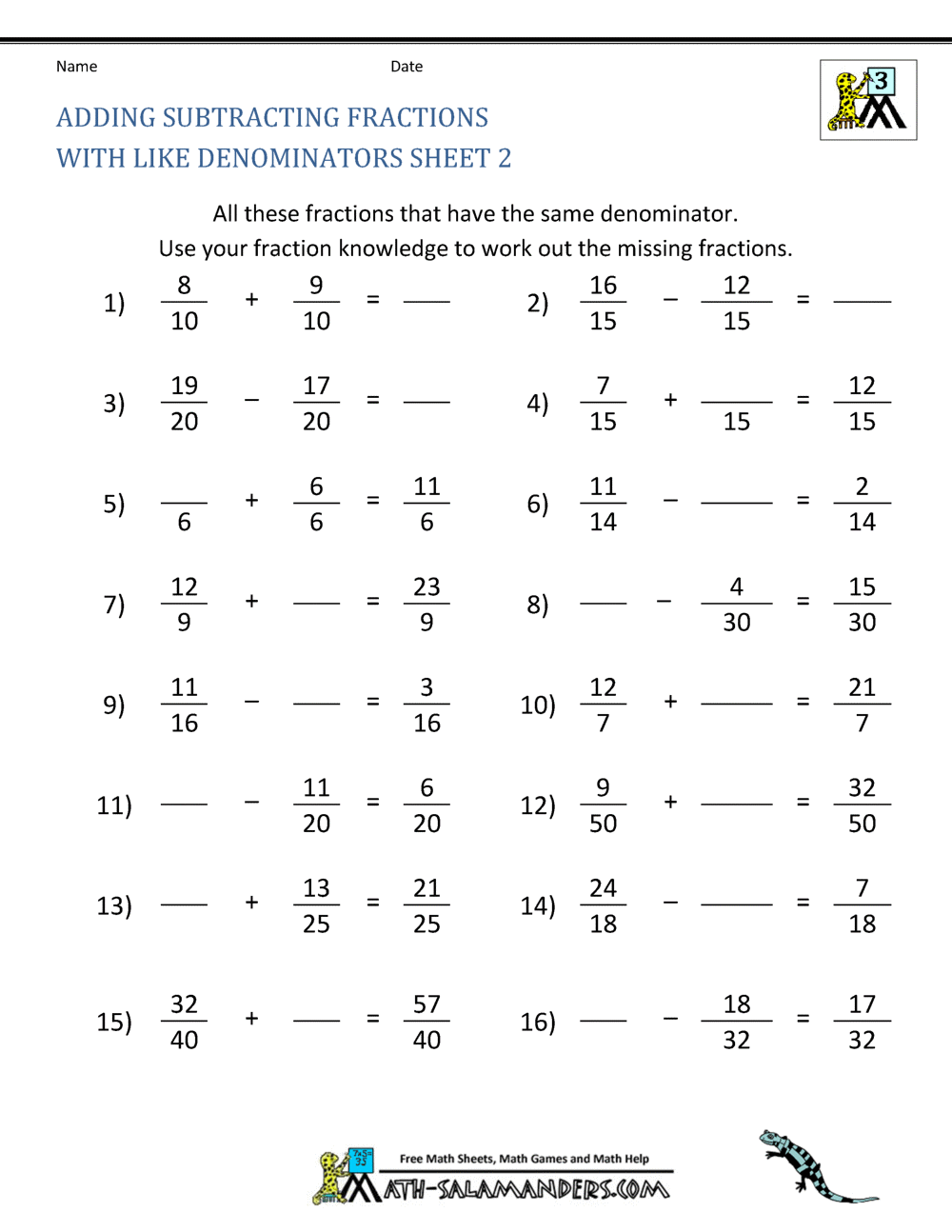Understanding how to add fractions to a whole number is a fundamental skill that can enhance your mathematical prowess. Whether you are a student grappling with basic arithmetic or an adult looking to refresh your skills, knowing how to combine fractions with whole numbers is essential. This knowledge not only serves you in academic settings but also in real-life situations, such as cooking, budgeting, and home improvement projects.
When faced with the task of adding fractions to a whole number, it’s crucial to grasp the underlying concepts that govern this operation. With the right approach, anyone can learn to perform this task with ease. This article aims to provide you with a comprehensive guide to adding fractions to whole numbers, breaking down the process into manageable steps. So, whether you're a parent helping a child with homework or simply trying to sharpen your own skills, you’ll find valuable insights here.
In this guide, we will cover various methods to add fractions to whole numbers, including practical examples and tips that simplify the learning process. By the end of this article, you’ll be equipped with the knowledge and confidence to tackle any problem involving the addition of fractions to whole numbers. Let’s dive into the world of fractions!
What are Fractions?
Fractions represent a part of a whole. They are composed of two parts: the numerator (the top number) and the denominator (the bottom number). Understanding fractions is vital as they help in quantifying parts of a whole, making them indispensable in everyday calculations.
What is a Whole Number?
Whole numbers are numbers without fractions or decimals. They are non-negative integers, including zero. Whole numbers are fundamental in mathematics and form the basis of counting and ordering.
How to Add Fractions to a Whole Number?
Adding fractions to a whole number can be straightforward if you follow these steps:
- Identify the whole number and the fraction you want to add.
- Convert the whole number to a fraction by giving it a denominator of 1.
- Find a common denominator if the fraction has a different denominator.
- Add the two fractions together.
- Simplify the resulting fraction if possible.
Can You Provide an Example of Adding Fractions to a Whole Number?
Certainly! Let’s say you want to add 2 to the fraction 1/4.
1. Convert 2 to a fraction: 2 = 2/1.
2. Find a common denominator: The least common denominator between 1 and 4 is 4.
3. Convert 2/1 to a fraction with a denominator of 4: 2/1 = 8/4.
4. Now, add the two fractions: 8/4 + 1/4 = 9/4.
5. Simplify if necessary: 9/4 can also be expressed as 2 1/4.
What if the Fraction is Improper?
Improper fractions occur when the numerator is greater than the denominator. For instance, if you want to add 3 to the fraction 5/4:
1. Convert 3 to a fraction: 3 = 3/1.
2. Find a common denominator: The least common denominator is still 4.
3. Convert 3/1 to a fraction with a denominator of 4: 3/1 = 12/4.
4. Add the two fractions: 12/4 + 5/4 = 17/4.
5. Simplify: 17/4 can also be expressed as 4 1/4.
Why is it Important to Learn Adding Fractions to a Whole Number?
Learning how to add fractions to a whole number is vital for various reasons:
- It enhances problem-solving skills.
- It is applicable in real-life scenarios.
- It forms a foundational skill for more complex mathematics.
What Tools Can Help You Master This Skill?
Several resources can assist in mastering the art of adding fractions to a whole number:
- Math textbooks and workbooks
- Online tutorials and videos
- Math games and apps
- Practice worksheets
How Can You Practice Adding Fractions to Whole Numbers?
Practice makes perfect! Here are some methods to hone your skills:
- Start with simple fractions and gradually increase complexity.
- Use real-life scenarios to apply what you've learned.
- Engage with peers or tutors for collaborative learning.
- Utilize online quizzes and exercises for self-assessment.
In conclusion, adding fractions to a whole number may seem daunting at first, but with practice and understanding, it becomes second nature. By mastering this skill, you’ll not only excel in mathematics but also gain confidence in your ability to tackle various real-world challenges. So grab your pencil and paper, and start practicing today!
Article Recommendations
- Gen Tullos
- Eau De Cologne Et Eau De Toilette
- Vogue October 2003
- Glenn Plummer
- Vegan Restaurants In Sugar Land
- Large Living Room Cabinet
- Zhang Xueying
- Freddie Prinze Jr Jessica Biel
- G3 Case
- Evergreen Bushes And Shrubs