Understanding the concept of arc length in a parametric context is crucial for anyone delving into the realms of calculus and geometry. This mathematical principle allows us to calculate the distance along a curve defined by parametric equations, which can often lead to more intricate and beautiful representations of curves compared to traditional Cartesian coordinates. As we embark on this exploration, we will uncover the significance of arc length parametric and its applications across various fields, including physics and engineering.
Arc length parametric not only provides a method for calculating distances along curves but also enhances our understanding of motion and change. The ability to express curves in a parametric form enables mathematicians and scientists to model real-world phenomena more accurately. By translating complex curves into manageable equations, we can analyze their properties, visualize their shapes, and apply this knowledge to solve practical problems.
In this article, we will walk you through the intricacies of arc length parametric, addressing common questions and providing clear explanations. Whether you are a student, educator, or simply someone with an interest in mathematics, this guide will equip you with the knowledge needed to navigate the arc length of parametric equations successfully.
What is Arc Length Parametric?
Arc length parametric refers to the calculation of the length of a curve described using parametric equations. In a parametric representation, both the x and y coordinates of points on the curve are expressed as functions of a third variable, typically denoted as 't'. The arc length can be derived using a specific formula that incorporates the derivatives of these functions. This method is particularly useful when dealing with curves that do not lend themselves easily to Cartesian coordinates.
How is Arc Length Parametric Calculated?
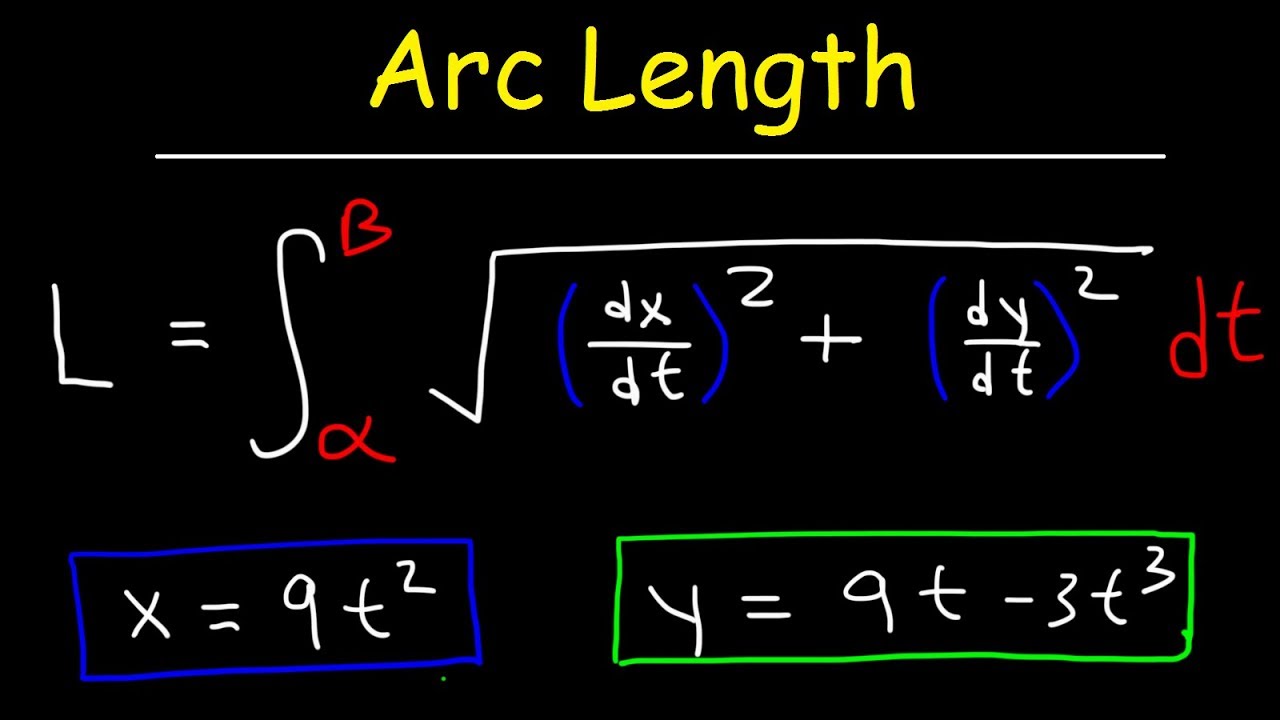
The formula for calculating the arc length (L) of a parametric curve defined by the equations x(t) and y(t) over an interval [a, b] is given by:
L = ∫ from a to b √(dx/dt)² + (dy/dt)² dt
Where:
- dx/dt is the derivative of x with respect to t.
- dy/dt is the derivative of y with respect to t.
- √ denotes the square root.
- ∫ signifies the integral symbol, which is used to calculate the area under the curve.
Why Use Parametric Equations for Arc Length?
Parametric equations provide a versatile way to describe curves, allowing for greater flexibility in modeling complex shapes. Some reasons to use parametric equations for arc length calculation include:
- Ability to represent curves that cannot be expressed as a function of y = f(x).
- Facilitates the analysis of motion along a path.
- Enhances visualization of curves in three-dimensional space.
What are Some Applications of Arc Length Parametric?
The applications of arc length parametric are vast and varied, spanning across different fields. Here are some notable uses:
- Physics: Analyzing trajectories of moving objects.
- Engineering: Designing curves in structures and materials.
- Computer Graphics: Rendering smooth curves in digital images.
Can You Provide an Example of Arc Length Parametric Calculation?
Certainly! Let’s consider a simple example of a parametric curve defined by the following equations:
- x(t) = t²
- y(t) = t³
We will calculate the arc length of this curve from t = 1 to t = 2.
First, we find the derivatives:
- dx/dt = 2t
- dy/dt = 3t²
Now we can plug these values into the arc length formula:
L = ∫ from 1 to 2 √((2t)² + (3t²)²) dt
This simplifies to:
L = ∫ from 1 to 2 √(4t² + 9t^4) dt
Calculating this integral will yield the length of the arc between the specified bounds.
What Challenges Might One Face in Arc Length Parametric Calculations?
While arc length parametric offers a powerful tool for curve analysis, it also presents challenges, including:
- Complex calculations, particularly for intricate curves.
- Difficulty in determining the limits of integration.
- Understanding the behavior of parametric equations over various intervals.
How to Visualize Arc Length in Parametric Curves?
Visualization plays a key role in comprehending arc length parametric. Here are some methods to visualize arc lengths:
- Graphing Software: Utilize graphing tools to plot parametric equations.
- Dynamic Geometry Software: Explore the relationship between parametric curves and their arc lengths.
- Animation: Create animations to illustrate how the arc length varies with changes in the parameter t.
Conclusion: The Importance of Understanding Arc Length Parametric
In conclusion, the concept of arc length parametric is a vital aspect of mathematics that goes beyond mere calculations. It opens the door to a deeper understanding of curves, motion, and real-world applications. By mastering this concept, individuals can enhance their analytical skills and apply them in various disciplines, from engineering to computer graphics. Embracing arc length parametric not only enriches one’s mathematical toolkit but also fosters a greater appreciation for the beauty of curves in our world.
Article Recommendations
- Price Tag Details
- Ixora Maui Yellow
- Freddie Prinze Jr Jessica Biel
- Glenn Plummer
- Evergreen Bushes And Shrubs
- Large Living Room Cabinet
- Reflex Compound Bow
- Encroachment Easement
- Amy Allan
- Emo In Thong