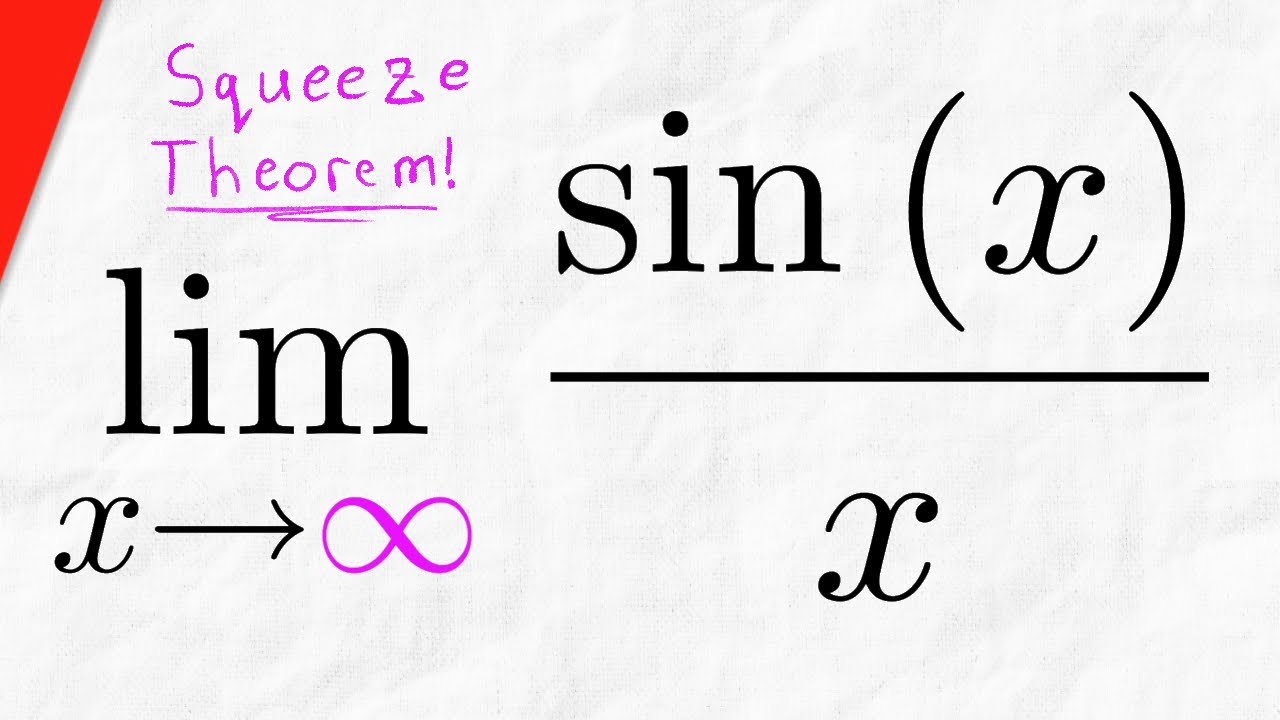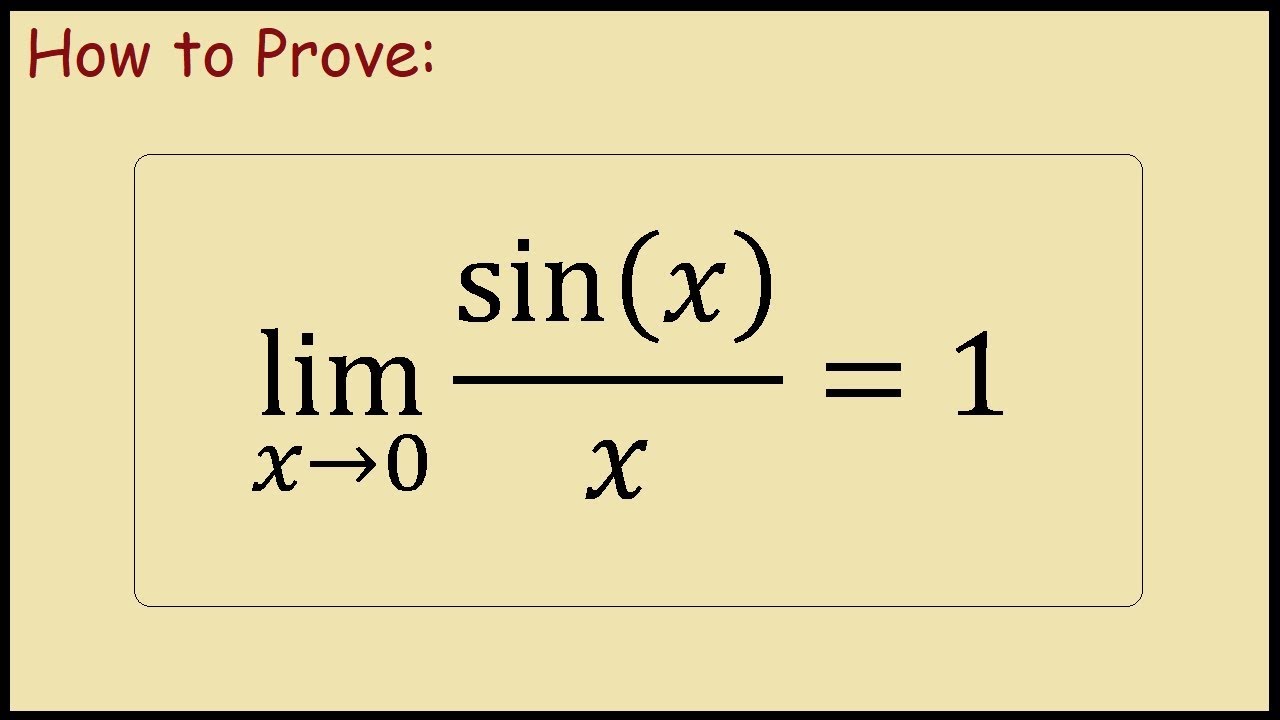The concept of limits is fundamental in calculus, and one of the most intriguing limits that students encounter is lim sin x / x. This limit serves as a cornerstone for several mathematical applications and provides a bridge between trigonometry and calculus. Notably, it plays a vital role in understanding continuity and differentiability in functions. This article aims to delve deep into the significance of this limit, elucidating its applications and the reasoning behind its value.
In the realm of mathematics, particularly in calculus, the limit of sin x / x as x approaches 0 has profound implications. It is a prime example of how trigonometric functions can behave in relation to polynomial functions. Understanding this limit not only shapes our comprehension of calculus but also enhances our problem-solving skills, especially in scenarios involving indeterminate forms. As we explore the essence of lim sin x / x, we will uncover its importance in various mathematical contexts.
Moreover, lim sin x / x is not merely an abstract concept but one that finds practical applications in physics, engineering, and computer science. Whether it’s analyzing wave functions, optimizing algorithms, or even modeling natural phenomena, this limit provides essential insights. Join us as we unravel the mysteries of lim sin x / x, shedding light on its theoretical underpinnings and real-world applications.
What is the Limit lim sin x / x?
The limit lim sin x / x as x approaches 0 is one of the foundational limits in calculus. It can be expressed mathematically as:
lim (x → 0) (sin x / x) = 1
This result is pivotal because it demonstrates that even though both the sine function and x approach 0, their ratio approaches a finite limit of 1. This limit is crucial when dealing with derivatives of trigonometric functions, particularly when applying L'Hôpital's Rule or Taylor series expansions.
How to Prove lim sin x / x = 1?
Several methods can be employed to prove the limit lim sin x / x = 1. Here are a few common approaches:
- Geometric Proof: Using the unit circle, one can visualize the relationship between the arc length and the sine function.
- Using L'Hôpital's Rule: This rule is applicable in this context since the limit results in the indeterminate form 0/0.
- Taylor Series Expansion: Expanding sin x using its Taylor series provides a straightforward approach to establish the limit.
What Does lim sin x / x Represent in Calculus?
The limit lim sin x / x represents the behavior of the sine function in relation to linear functions as x approaches 0. It indicates that near the origin, the sine function behaves almost like the identity function. This insight is critical when analyzing the continuity and differentiability of the sine function.
Why is lim sin x / x Important in Real-World Applications?
The significance of lim sin x / x extends beyond theoretical mathematics; it finds practical applications in various fields:
- Physics: In wave mechanics, understanding the behavior of oscillations requires knowledge of this limit.
- Engineering: Signal processing often utilizes trigonometric functions where this limit becomes essential in signal approximation.
- Computer Science: Algorithms that involve trigonometric calculations can benefit from the properties established by this limit.
How to Apply lim sin x / x in Problem Solving?
When faced with problems that involve the limit lim sin x / x, the following strategies can be useful:
- Identify whether the limit approaches an indeterminate form.
- Consider applying L'Hôpital's Rule if applicable.
- Utilize Taylor series expansions for approximations.
- Always visualize the problem geometrically, if possible, to gain intuitive insights.
What Are Some Common Misconceptions About lim sin x / x?
Several misconceptions often arise when discussing lim sin x / x:
- Many believe that the limit only holds true for small values of x, but it is a universal property of the sine function.
- Some may confuse the limit with the value of sin x at 0, forgetting that limits and function values can behave differently.
- Others might overlook the significance of this limit in higher dimensions, particularly in multivariable calculus.
Conclusion: Why Should You Care About lim sin x / x?
Understanding lim sin x / x is essential for anyone delving into calculus and its applications. This limit not only serves as a fundamental building block for more complex mathematical concepts but also aids in grasping the relationship between different types of functions. In a world where mathematics plays a crucial role in various fields, having a firm grasp of such limits can significantly enhance one’s analytical and problem-solving skills.
Ultimately, the limit lim sin x / x is much more than a simple mathematical expression; it is a gateway to deeper understanding and appreciation of the interconnectedness of mathematical concepts. Embracing this knowledge will undoubtedly benefit students, professionals, and enthusiasts alike in their mathematical journeys.
Article Recommendations
- Brown Tweed Suit Wedding
- Vegan Restaurants In Sugar Land
- Amy Allan
- Fernando Godoy
- Eau De Cologne Et Eau De Toilette
- Vogue October 2003
- 3 Way Wiring Diagram
- Gotlet
- Elasticized Belt
- Mexican Pot Luck