When it comes to geometry, triangles are one of the most fundamental shapes, making their area calculation a crucial skill in mathematics. Among various methods to compute the area of a triangle, using the sine function stands out for its elegance and practicality. This method is particularly useful when you know two sides of the triangle and the angle between them, providing a straightforward way to determine the area without needing to know the altitude.
In this article, we will delve into the fascinating world of triangle area calculations, focusing on the sine function. We will explore how this mathematical concept is applied in various scenarios, from academic purposes to real-world applications. By the end of this discussion, you will have a comprehensive understanding of how to calculate the area of a triangle using the sine function, enhancing your mathematical toolkit.
Whether you are a student grappling with geometry or a professional needing to apply these principles in engineering or architecture, understanding the triangle area using sine is invaluable. Let’s embark on this enlightening journey into the realm of triangles and their properties!
What is the Formula for Calculating Triangle Area Using Sine?
The formula to calculate the area of a triangle using the sine function is straightforward and can be expressed as:
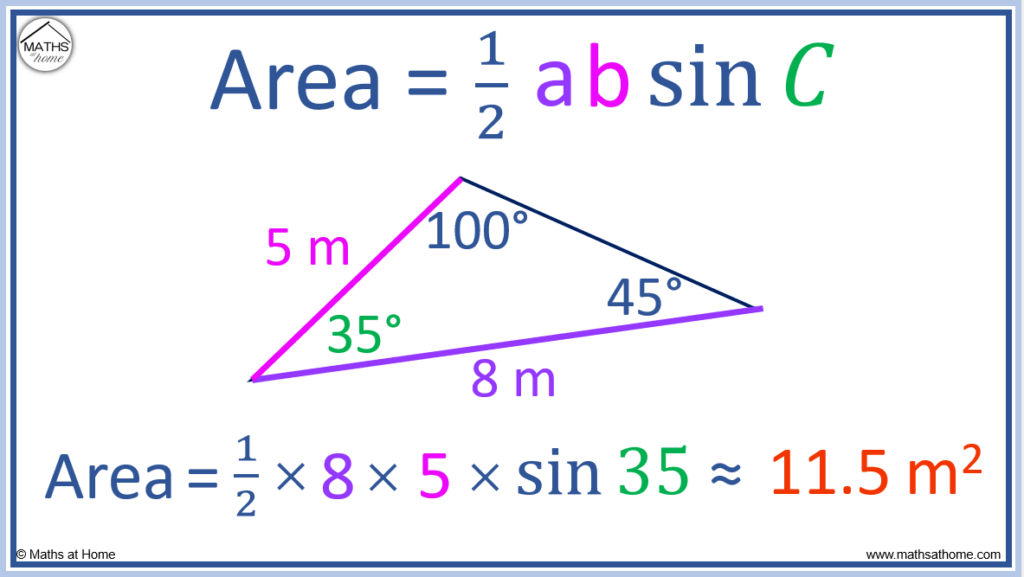
Area = 0.5 × a × b × sin(C)
Where:
- a = length of one side of the triangle
- b = length of the other side of the triangle
- C = angle between sides a and b in degrees or radians
Why Use the Sine Function for Triangle Area Calculation?
Using the sine function for calculating the area of a triangle provides several advantages:
- Works with known angles and two sides
- Applicable to all types of triangles (acute, obtuse, right)
- Simplifies calculations in trigonometric contexts
How Does the Sine Function Relate to Triangles?
The sine function is a fundamental concept in trigonometry, representing the ratio of the length of the opposite side to the hypotenuse in a right triangle. This relationship is crucial when working with triangles, as it allows us to understand the geometric properties better and apply them in various calculations.
Can You Provide an Example of Triangle Area Calculation Using Sine?
Absolutely! Let’s consider a triangle with sides a = 5 units, b = 7 units, and the angle C = 30 degrees. Using the formula mentioned earlier:
Area = 0.5 × 5 × 7 × sin(30)
Calculating this:
- sin(30) = 0.5
- Area = 0.5 × 5 × 7 × 0.5 = 8.75 square units
This example illustrates how efficiently the sine function can be used to determine the area of a triangle when specific measurements are known.
What Are Other Methods to Calculate Triangle Area?
In addition to the sine method, there are several other ways to calculate the area of a triangle:
- Base and Height Method: Area = 0.5 × base × height
- Heron’s Formula: Area = √(s × (s-a) × (s-b) × (s-c)), where s = (a+b+c)/2
- Coordinate Geometry: For triangles defined by coordinates, the area can be calculated using the formula: Area = 0.5 × |x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
How Do Real-World Applications of Triangle Area Using Sine Function Work?
The application of triangle area calculations using the sine function extends to various fields:
- Architecture: Designing structures often requires area calculations for triangular sections.
- Engineering: Mechanical and civil engineers frequently use these calculations in project designs.
- Navigation: Sailors and pilots apply trigonometric principles, including triangle area calculations, for route planning and positioning.
What Resources Can Help You Master Triangle Area Calculations?
To master the calculations involving triangle areas using the sine function, consider the following resources:
- Textbooks on Trigonometry: These provide in-depth explanations and examples.
- Online Tutorials: Websites like Khan Academy offer free courses on the topic.
- Mathematics Software: Tools like GeoGebra can help visualize and compute areas.
Are There Common Mistakes to Avoid When Calculating Triangle Area?
Yes, there are several common pitfalls to be aware of:
- Misidentifying the angle or sides when applying the sine formula.
- Forgetting to convert angles from degrees to radians or vice versa, depending on the calculator being used.
- Mixing up the values of sides a and b, leading to calculation errors.
Conclusion: Why is Understanding Triangle Area Important?
Understanding how to calculate the triangle area using the sine function is essential for anyone engaged in mathematics, engineering, or any field that relies on geometric principles. Mastery of this concept not only enhances your problem-solving skills but also equips you with the tools necessary to approach more complex mathematical challenges. With practice and application, you will find that the knowledge of triangle area calculations becomes a powerful asset in your academic and professional endeavors.
Article Recommendations
- Lisa Raye Height
- Semi Gloss Polyurethane
- Chelsea Hobbs
- Opera Singer Marina Viotti
- Reflex Compound Bow
- Ap Precalculus Unit 3 Review
- Sherell Ford
- Tornado Pro 4 Jacket
- Bi Fold Exterior Patio Doors
- 80s High Waisted Bikini