The Dirac distribution, also known as the Dirac delta function, is a mathematical construct that has profound implications in the fields of physics, engineering, and applied mathematics. This distribution is not just a simple function but rather a powerful tool used to model and analyze a variety of phenomena, from signal processing to quantum mechanics. Its unique properties allow for the representation of point sources and instantaneous impulses, making it an essential concept in many scientific areas.
In essence, the Dirac distribution acts as a theoretical representation of a point mass or point charge in space, concentrated at a specific location. This characteristic makes it invaluable in situations where we want to describe the behavior of systems undergoing sudden changes or events. As we delve deeper into the world of the Dirac distribution, we will uncover its mathematical foundations, applications, and significance in various disciplines.
Understanding the Dirac distribution is crucial for students and professionals alike, as it serves as a stepping stone to more complex theories and applications. Its use in differential equations, Fourier transforms, and other mathematical analyses highlights the need for a comprehensive grasp of this concept. In the following sections, we will explore the Dirac distribution in greater detail, answering common questions and shedding light on its pivotal role in modern science and engineering.
What is the Dirac Distribution?
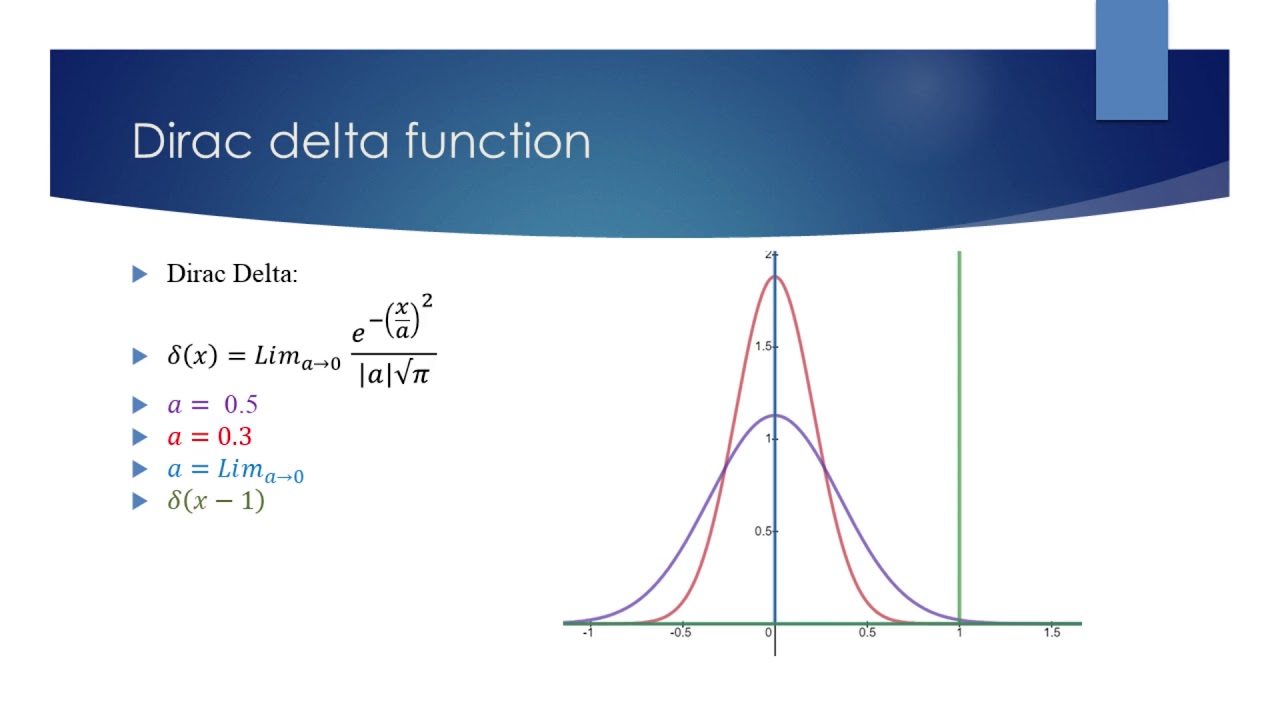
The Dirac distribution is a mathematical function that is defined to be zero everywhere except at a single point, where it is infinitely high, and its integral over the entire space is equal to one. This makes it an idealized representation of an impulse or a point mass. The Dirac delta function is often expressed as δ(x), and it is widely used in various branches of mathematics and physics.
How is the Dirac Distribution Mathematically Represented?
The mathematical representation of the Dirac distribution can be understood through the following properties:
- For any continuous function f(x), the integral of f(x) multiplied by the Dirac delta function over the entire space yields the value of f at the point of interest:
∫ f(x) δ(x - a) dx = f(a)
- The Dirac delta function is defined such that:
δ(x) = 0 for x ≠ 0 and ∫ δ(x) dx = 1
What Are the Applications of Dirac Distribution?
The Dirac distribution has numerous applications across various fields:
- Signal Processing: It is used to model impulse signals in electronic systems.
- Quantum Mechanics: The Dirac delta function is essential in quantum field theory, especially in defining states and operators.
- Control Systems: It aids in the analysis of systems that react instantaneously to inputs.
- Mathematical Analysis: It simplifies the solving of differential equations through convolution and Fourier transforms.
Who is Paul Dirac?
To fully appreciate the Dirac distribution, one must understand the man behind the concept, Paul Dirac. Born in 1902, Dirac was a theoretical physicist who made groundbreaking contributions to quantum mechanics and quantum electrodynamics, earning him the Nobel Prize in Physics in 1933.
What Were the Contributions of Paul Dirac?
Dirac's work laid the foundation for modern quantum mechanics. His most notable contributions include:
- The Dirac equation, which describes the behavior of fermions and predicted the existence of antimatter.
- The formulation of quantum field theory, which describes how particles interact at a fundamental level.
- The introduction of the Dirac distribution, which is crucial for understanding point-like sources in physics.
Paul Dirac's Personal Details and Bio Data
| Name | Paul Dirac |
|---|---|
| Birth Date | August 8, 1902 |
| Birth Place | Bradford, England |
| Field of Study | Theoretical Physics |
| Nobel Prize | Physics, 1933 |
| Death Date | October 20, 1984 |
Why is the Dirac Distribution Important in Physics?
The importance of the Dirac distribution in physics cannot be overstated. It provides a mathematical framework for analyzing systems that exhibit instantaneous changes. For example, in classical mechanics, the Dirac delta function can model a collision between two particles, allowing physicists to study the subsequent motion of the system.
How Does the Dirac Distribution Relate to Fourier Transforms?
Fourier transforms are a powerful mathematical tool used to analyze signals in the frequency domain. The Dirac distribution plays a crucial role in Fourier analysis because it serves as a bridge between time-domain and frequency-domain representations. The Fourier transform of the Dirac delta function is a constant function, illustrating its significance in signal processing.
What Are Some Common Misconceptions About the Dirac Distribution?
Despite its widespread use, several misconceptions about the Dirac distribution persist:
- It is a function: The Dirac delta function is actually a distribution, not a traditional function.
- It can be evaluated at a point: The Dirac delta function does not have a defined value at any point except in the context of an integral.
- It is only applicable in physics: While it is widely used in physics, the Dirac distribution has applications in engineering and mathematics as well.
How Can One Learn More About the Dirac Distribution?
To gain a deeper understanding of the Dirac distribution, consider the following resources:
- Textbooks on Mathematical Analysis: Many advanced mathematics textbooks cover distributions and the Dirac delta function in detail.
- Online Courses: Platforms like Coursera and edX offer courses in mathematics, physics, and engineering that include sections on distributions.
- Research Papers: Reading academic papers that utilize the Dirac distribution can provide real-world examples of its applications.
In conclusion, the Dirac distribution is a versatile and powerful mathematical tool that plays a critical role in various scientific fields. By understanding its properties, applications, and the legacy of Paul Dirac, one can appreciate the importance of this concept in both theoretical and practical contexts. Whether you are a student, a researcher, or simply curious about mathematical concepts, exploring the Dirac distribution offers a fascinating glimpse into the interplay of mathematics and physics.
Article Recommendations
- Elasticized Belt
- Gen Tullos
- Bec And Bridge Bridesmaid
- Tornado Pro 4 Jacket
- Cartel Murder Photos
- Kobe Thai
- Brown Tweed Suit Wedding
- Old Dollar Shave Club Handle
- Price Tag Details
- Gta Iv Script Hook

:max_bytes(150000):strip_icc()/1300px-Dirac_distribution_PDF.svg-56aeb7423df78cf772bd6898.png)