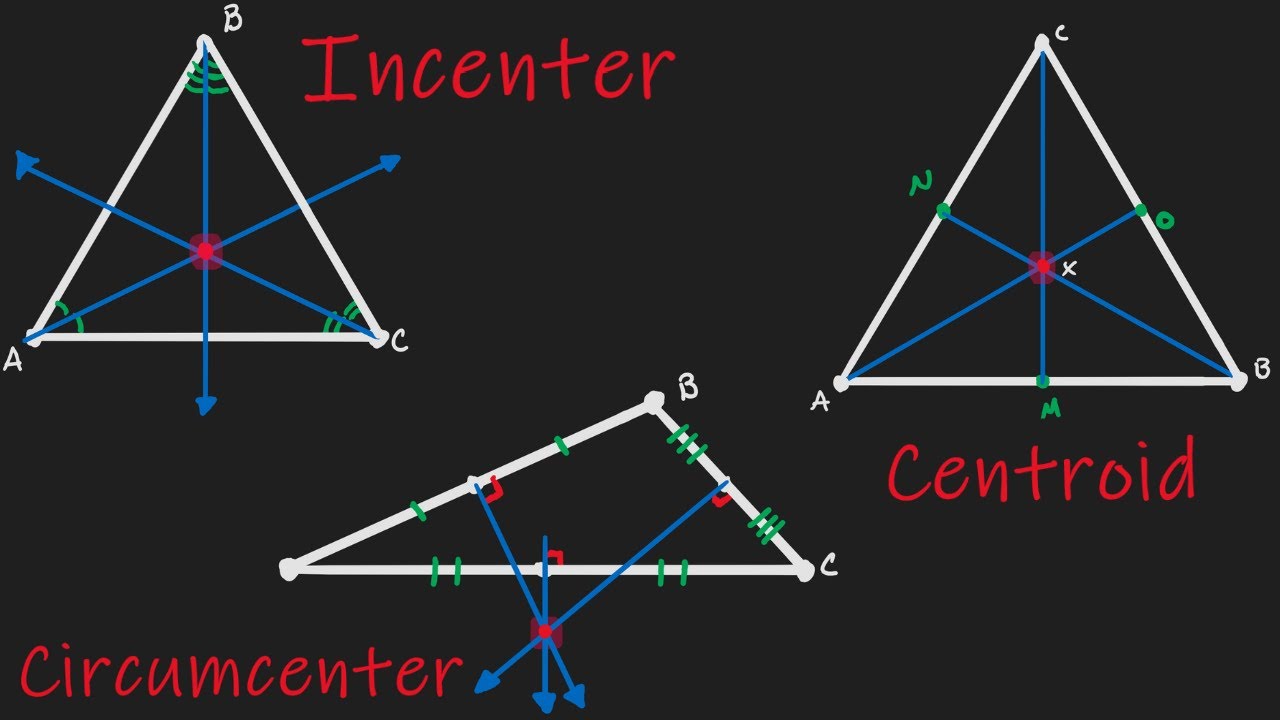
The study of geometry introduces us to fascinating concepts that form the backbone of many mathematical principles. Among these concepts, the terms "centroid" and "circumcenter" often arise, prompting curiosity and sometimes confusion. While both are points associated with triangles, they serve different purposes and have unique properties. Understanding these differences can enhance our grasp of geometric concepts and improve our problem-solving skills in various applications.
In the realm of triangles, the centroid and circumcenter are key points that contribute to the shape and structure of the triangle. The centroid, often referred to as the "center of mass," is the point where the three medians of a triangle intersect. On the other hand, the circumcenter is the point where the perpendicular bisectors of the sides meet, and it serves as the center for the circumcircle—the circle that passes through all three vertices of the triangle. This article will delve into the intricacies of these two essential points, comparing and contrasting their properties, calculations, and applications.
As we explore the relationship between centroid vs circumcenter, we will answer common questions, provide detailed explanations, and offer examples to clarify these geometric concepts. By the end of this article, you will have a solid understanding of both points and be able to distinguish between them with confidence.
What is a Centroid?
The centroid is the point of concurrency of the medians of a triangle. Medians are line segments that connect each vertex of the triangle to the midpoint of the opposite side. Here are some key properties of the centroid:
- The centroid divides each median into a ratio of 2:1, with the longer segment being closer to the vertex.
- It is always located inside the triangle, regardless of the triangle's type (acute, obtuse, or right).
- The coordinates of the centroid can be calculated using the formula:
G(x,y) = ((x1 + x2 + x3)/3 , (y1 + y2 + y3)/3)
What is a Circumcenter?
The circumcenter, unlike the centroid, is the point where the perpendicular bisectors of the sides of a triangle intersect. This point has its own unique properties:
- The circumcenter can be located inside, outside, or on the triangle, depending on the type of triangle.
- It is the center of the circumcircle, which is the circle that passes through all three vertices of the triangle.
- The circumcenter can be found using the formula:
C(x,y) = (x1+x2+x3)/3 , (y1+y2+y3)/3 (for a triangle defined by its vertices).
What are the Key Differences Between Centroid and Circumcenter?
When comparing centroid vs circumcenter, we can highlight several key differences:
- Definition: The centroid is the intersection of the medians, while the circumcenter is the intersection of the perpendicular bisectors.
- Location: The centroid is always inside the triangle, whereas the circumcenter can be outside, inside, or on the triangle.
- Purpose: The centroid represents the center of mass, while the circumcenter represents the center of the circumcircle.
How to Find the Centroid of a Triangle?
Finding the centroid is relatively straightforward. Here’s a step-by-step approach:
- Identify the coordinates of the vertices of the triangle, denoted as (x1, y1), (x2, y2), and (x3, y3).
- Use the centroid formula to calculate the coordinates of the centroid:
G(x,y) = ((x1 + x2 + x3)/3 , (y1 + y2 + y3)/3) - The resulting point (Gx, Gy) is the centroid of the triangle.
How to Find the Circumcenter of a Triangle?
Finding the circumcenter involves a bit more geometry. The steps are as follows:
- Identify the coordinates of the triangle's vertices (x1, y1), (x2, y2), and (x3, y3).
- Calculate the midpoints of at least two sides of the triangle.
- Determine the slopes of the sides and find the perpendicular slopes.
- Using the midpoints and perpendicular slopes, write the equations of the perpendicular bisectors.
- Solve the equations simultaneously to find the intersection point, which will be the circumcenter.
What Are the Applications of Centroid and Circumcenter?
Both the centroid and circumcenter have practical applications in various fields:
- Engineering: The centroid helps in determining the center of mass for structural analysis.
- Computer Graphics: The centroid is used for object manipulation and collision detection.
- Navigation: The circumcenter is utilized in triangulation methods for determining locations.
Can Centroid and Circumcenter Be the Same Point?
In certain types of triangles, specifically equilateral triangles, the centroid and circumcenter coincide. This means they share the same coordinates, emphasizing the symmetry present in equilateral triangles. Understanding this relationship can further deepen our comprehension of these geometric concepts.
In conclusion, the comparison of centroid vs circumcenter reveals two distinct yet significant points in the study of triangles. While they share some similarities, their definitions, properties, locations, and applications set them apart. By grasping these differences and learning how to calculate each point, we can enhance our understanding of geometry and its practical implications in various fields.
Article Recommendations
- Drinking Ambien
- Tornado Pro 4 Jacket
- Ixora Maui Yellow
- Freddie Prinze Jr Jessica Biel
- Cleaning Kenmore Dishwasher
- Eau De Cologne Et Eau De Toilette
- Hdfs Copy To Local
- Sherell Ford
- Thyronorm 50mcg
- Bec And Bridge Bridesmaid